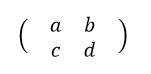
行列とは数字などを縦と横に並べて括弧で閉じたものです。
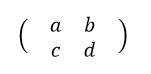
横方向を「行」、縦方向を「列」と呼びます。
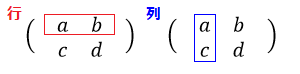
最初の式は2行2列(2×2)の行列となり、
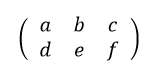
この式は2行3列(2×3)行列となります。
行の数と列の数が同じ行列を「正方行列」と言い、単位行列は正方行列です。
要素は0と1のみであり、行番号と列番号が同じ個所のみ1でそれ以外は0となります。
次の行列は2×2と3×3の単位行列です。
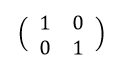

単位行列は行列の乗算における「単位元」となります。
行列同士の加減算は行数、列数が同じ行列同士でなければ計算できません。
加減算できる例 2行2列+2行2列
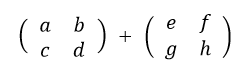
加減算できない例 2行2列+3行2列
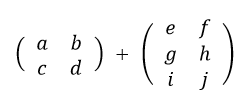
計算方法は、下の式のように、同じ行、同じ列の数字を加減算すれば良いだけです。
行列同士の加算
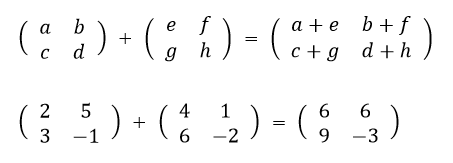
行列同士の減算
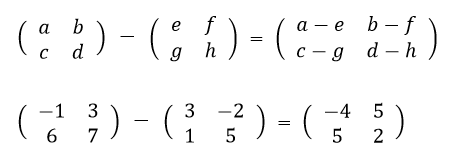
行列のスカラー倍とは、行列にスカラー(数)を乗算したものです。
下の式のように、各要素に数を乗算するだけでOKです。
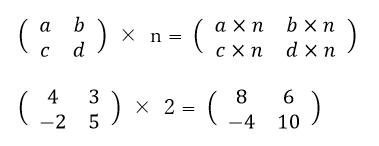
行列同士の乗算は、左辺の列数と右辺の行数が同じでなければ計算できません。
下の式は、1行2列×1行2列の行列同士の乗算ですが、左辺の列数は2、右辺行数は1ですから乗算できません。
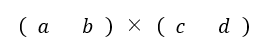
次の式も、左辺の列数は2、右辺の行数は3ですから乗算できません。
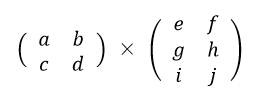
次の式は、左辺の列数が2、右辺の行数も2ですから乗算可能です。
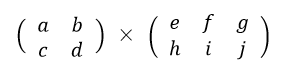
行列同士の乗算の計算方法は次のようになります。
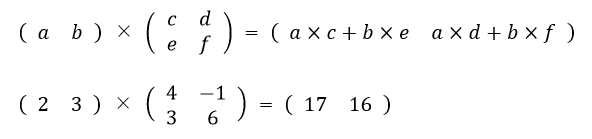
まず、覚えて欲しいのは「結果は左辺の行数×右辺の列数の行列になる」ことです。
上の式は、1行2列×2行2列の乗算ですが、結果は左辺の1行と右辺の2列の行列となっています。
もう少し例を見てみましょう。
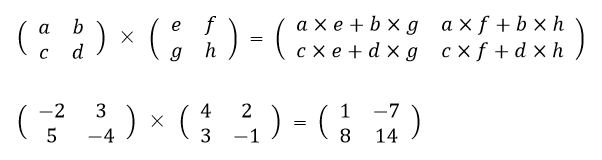
2行2列同士の乗算では、左辺の2行と右辺の2列という結果になります。
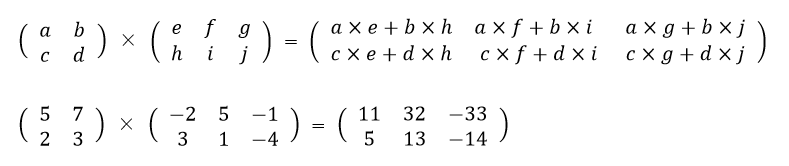
2行2列×2行3列の乗算は、左辺の2行右辺の3列で2行3列の行列ができます。
行列同士の乗算を行う場合、A×BとB×Aの結果が異なる場合があります。
次の例を見てください。
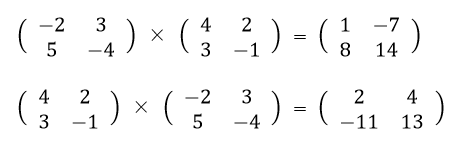
乗算の順番によって、結果が異なっています。
転置行列とは、行列の行と列を入れ替えた行列です。
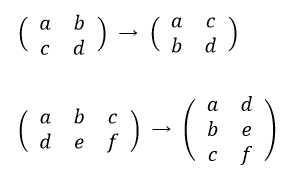
正方行列では行と列の数は変わりませんが、2行3列などの行列の場合3行2列の行列となります。
ある行列Aに別の行列Bを乗算した結果「単位行列」になる行列を「正則行列」と言います。
この時、行列Bを行列Aの「逆行列」と呼びます。
※説明には2行2列の行列を使います。
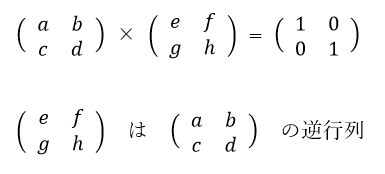
逆行列は必ず存在している訳ではなく、次の行列には逆行列はありません。
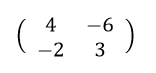
逆行列が存在するかどうかを調べるには、次の式で求められます。
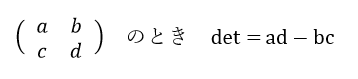
detとはdeterminant(デターミナント)の略で「行列式」といいます。
このdetの値が0の場合、逆行列は存在しません。
実際に計算してみると、
逆行列が存在しないケース
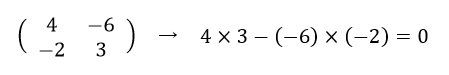
逆行列が存在するケース
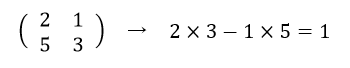
となります。
2行2列の逆行列は、
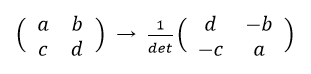
で求められます。(detは上で説明した「行列式」です)
実際に計算すると
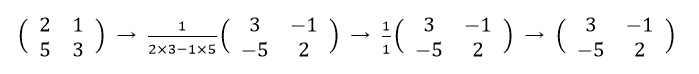
のようになります。
本当に逆行列になっているかどうか確かめてみましょう。
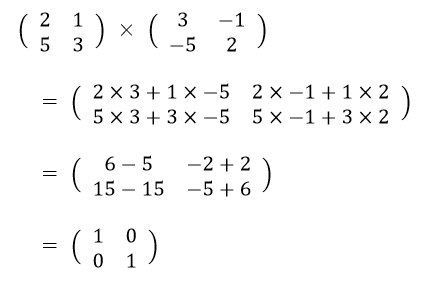
ちゃんと単位行列になりました。
次は3行3列の逆行列について説明します。
これからは位置関係が分かりづらくなるため、行列番号で表現します。
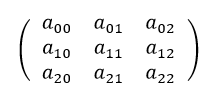
まず、逆行列が存在するかどうかは次の式で求めます。
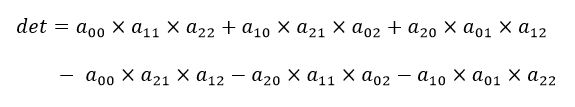
2行2列のときと同じくdetの値が0の場合、逆行列は存在しません。
逆行列を求める公式は、
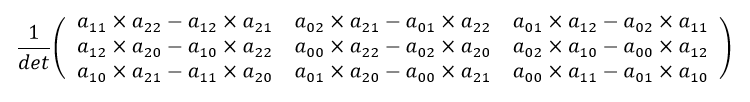
となります。
最後に4行4列の逆行列について説明します。

まず、逆行列が存在するかどうかは次の式で求めます。
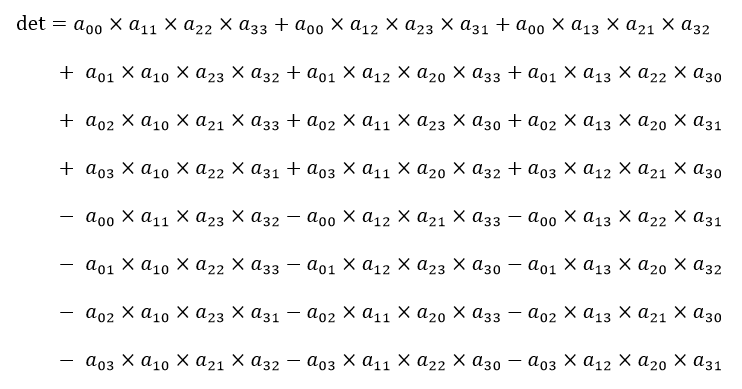
detの値が0の場合、逆行列は存在しません。
逆行列を求める公式は、
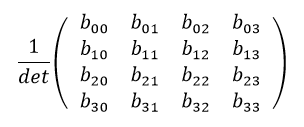
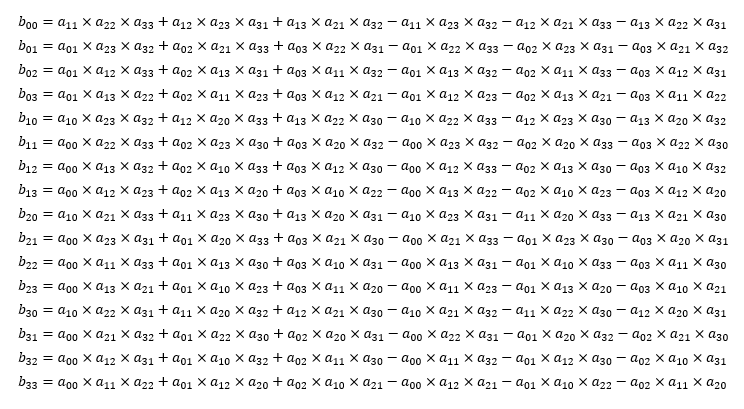
となります。
ベクトルと行列を乗算することで、ゲームなどで使える計算を行うことができます。
2Dベクトルは(x、y)で表されますが、1行2列の行列と見ることもできます。
であれば、2行の行列と乗算可能です。
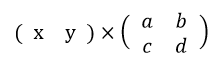
2Dベクトルの回転を行う公式は、
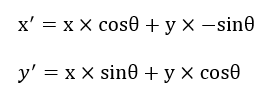
です。
これを行列に置き換えてみると
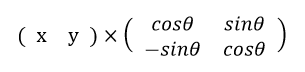
となり、展開すると同じ計算になります。
※DirectXを意識した向きで書いています。
回転だけであれば行列を使わなくても良いと思いますが、様々な動きを組み合わせたい場合は行列を使った方が良い場合もあります。
2Dベクトルの変換行列は3行3列の行列となります。
下の式は「単位行列」であり、回転も移動も拡大縮小もしない変換行列です。

例えば上で出てきた回転行列を変換行列に当てはめてみると、
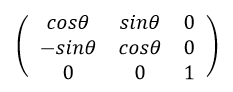
となり、この行列と2Dベクトルを乗算することで、回転させることができます。
が、2Dベクトルは1行2列の行列、変換行列は3行3列の行列であり、左辺(ベクトル)の列数が2、右辺の行数が3ですからこのままでは乗算できません。
そこで、ベクトルの方に「同次座標」で表し、3つ目の列を付け加えます。
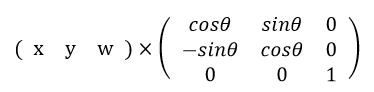
こうすればベクトルの列数は3、行列の行数も3となり乗算可能になります。
※同時座標は次元数を増やすことだと思ってください。 wには通常1が入ります。
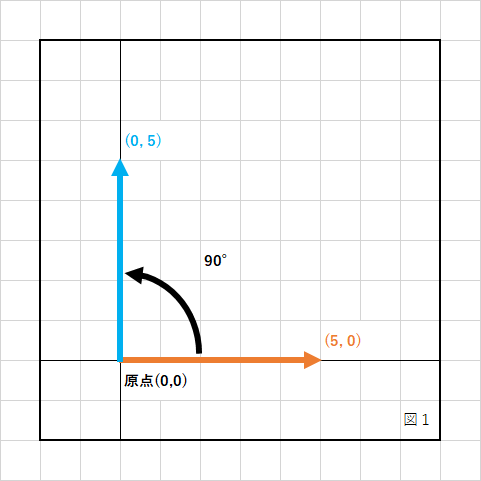
例として、ベクトル(5,0)を反時計回りに90°回転させてみます。
cos90°は0、sin90°は1ですから、変換行列は下のようになります。
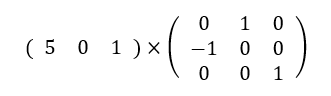
実際に計算してみると、
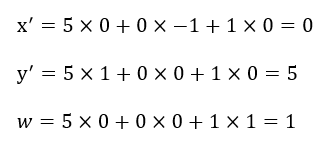
となり、回転後の座標は(0,5)となっています。
次に平行移動の変換行列を書きます。
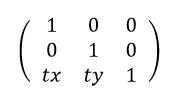
txにはX軸の移動量、tyにはY軸の移動量を入れます。
例として、現在地(5,0)からXの+方向に2、Yのマイナス方向に1移動する計算を行ってみます。
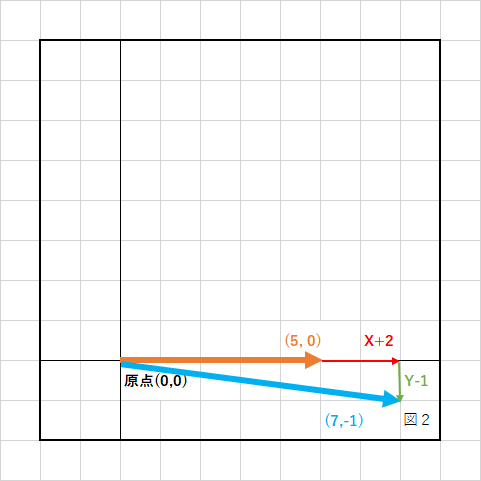
式は下のようになり、
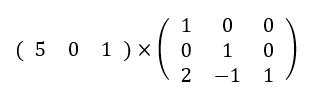
実際に計算してみると、
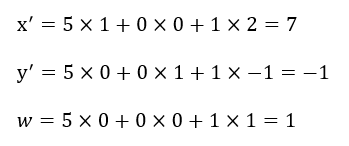
となり、移動後の座標は(7、−1)となっています。
異なる変換行列を組み合わせることで、新しい変換行列を作ることもできます。
変換行列を組み合わせるには、単純に変換行列同士を乗算すれば良いだけです。
上の例で紹介した、回転行列と平行移動行列を組み合わせてみましょう。

乗算する順番が異なると結果が異なることは以前説明しました。
今回は「回転行列」×「平行移動行列」の順に乗算しましたので「回転した後に平行移動する行列」になっています。
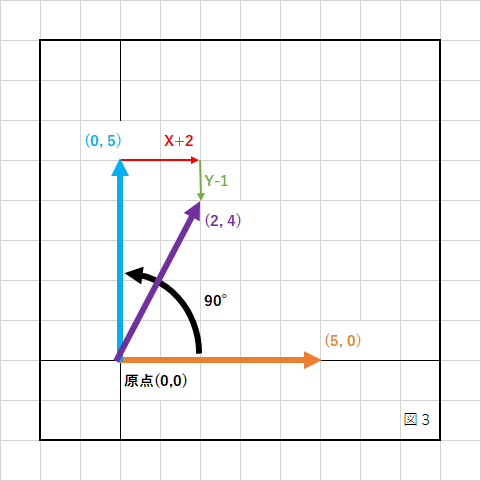
原点を中心に反時計回りに90°回転した後、Xの+方向に2、Yの−方向に1移動する行列です。
早速確かめてみるため式を書いてみます。
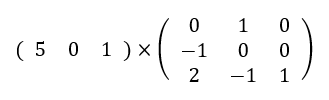
実際に計算してみると、
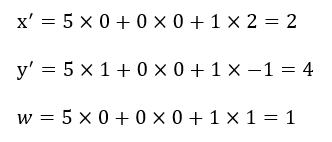
となり、正しく計算できていることが分かります。
最後に拡大縮小行列を説明します。

例として、座標(2,4)を原点を中心としてX方向に2倍、Y方向に0.5倍してみます。
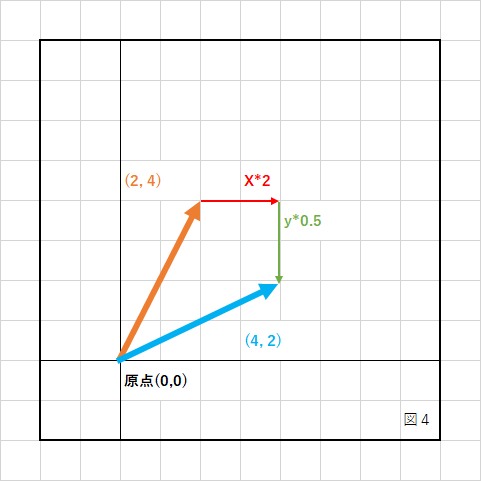
式は、
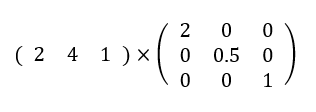
となり、実際に計算してみると、
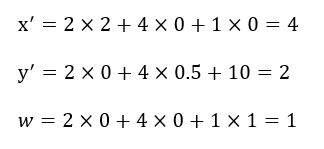
となり、正しく計算できていることが分かります。