
ベクトルはゲーム制作において重要な考え方であり、3Dゲーム制作においては必須の知識となります。
基本的には「位置」「方向」「大きさ」で表され、直感的に理解しやすくするため「矢印」で表現されています。
いきなり3次元は難しいので、2次元で説明します。

2次元座標の場合、ベクトルは(X,Y)で表されます。
この図の始点と終点が「位置」を、矢印が「方向」を、矢印の長さが「大きさ」を表します。
ベクトルをC言語の構造体で表現すると、
struct Vector2
{
float x;
float y;
};
|
のようになります。
※ここでは、DirectXを意識してdoubleではなくfloatで計算しますが、doubleの方が精度が高いので、より正確な計算を行う場合はdoubleで計算しましょう。
ベクトルの矢印部分は図2のようにX成分、Y成分で表すことができます。
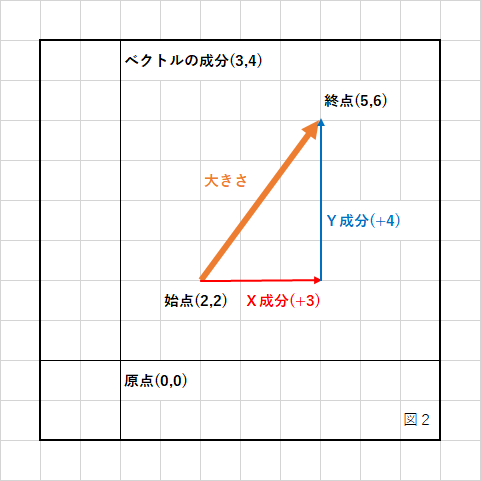
成分自体は始点と終点から求めることができます。
X成分 = 終点のX座標 − 始点のX座標 Y成分 = 終点のY座標 − 始点のY座標
C言語で書くと、
//始点
struct Vector2 start = { 2, 2 };
//終点
struct Vector2 end = { 5, 6 };
//成分
struct Vector2 components;
//成分計算
components.x = end.x - start.x;
components.y = end.y - start.y;
|
となります。
ベクトルの「大きさ」を求めるには、三平方の定理を使います。
図2の場合、x成分とy成分から、
大きさの2乗 = X成分の2乗 + Y成分の2乗 大きさ = 大きさの2乗の平方根
と求めることができます。
C言語で書くと、
#include <math.h> //大きさの計算 float magnitude = (float)sqrt(components.x * components.x + components.y * components.y); |
となります。
図2の例では、X成分が+3、Y成分が+4なので、
magnitude = sqrt(3 * 3 + 4 + 4); magnitude = sqrt(25); magnitude = 5
となります。
「大きさ」が1のベクトルを【単位(Identity)ベクトル】と言います。
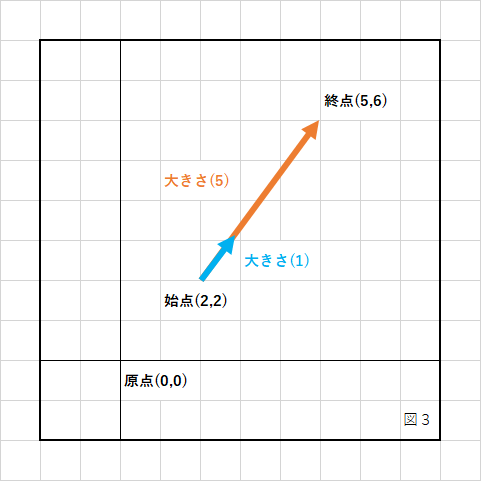
「方向」を使った計算には必ず必要な知識ですが、ベクトルの大きさを1にすることを正規化と言います。
正規化は以下の式で行います。
正規化後のX成分 = 正規化前のX成分 / 正規化前の大きさ 正規化後のY成分 = 正規化前のY成分 / 正規化前の大きさ
C言語で書くと、
//単位ベクトル struct Vector2 identity; //正規化 identity.x = components.x / magnitude; identity.y = components.y / magnitude; |
となり、図3の例で計算してみると、
identity.x = 3 / 5; identity.y = 4 / 5; identity.x = 0.6; identity.y = 0.8;
となります。
ちゃんと大きさが1になっているかどうか確かめると、
0.6 * 0.6 = 0.36 0.8 * 0.8 = 0.64 0.36 + 0.64 = 1 √1 = 1
大丈夫ですね。
単位ベクトルを「方向(Direction)」として使う場合、様々な使い道があります。
ゲームにおける移動もその1つです。
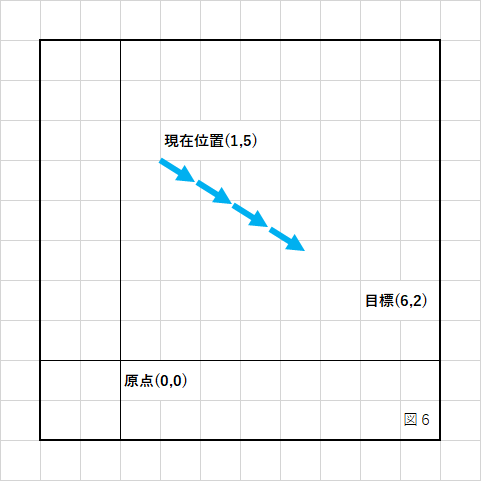
例えば「目標地点に徐々に近づいていく」という動きを考えてみます。
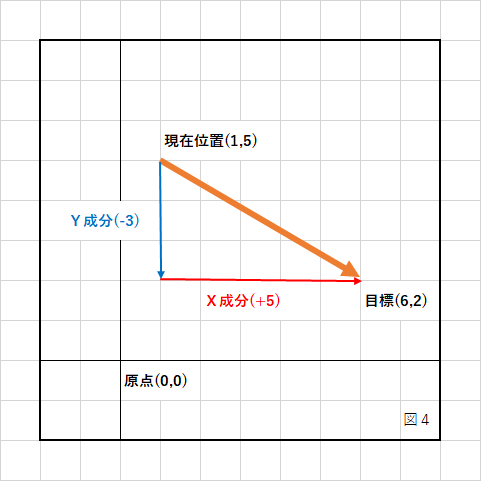
現在位置が(1,5)、目標地点が(6,2)で、X成分が+5、Y成分は−3です。
この現在位置から目標地点に向かって1だけ進ませるには、現在位置に「方向」を表した単位ベクトルを加算すればOKです。
では、移動後の座標を計算してみましょう。
現在地点から目標地点へのベクトルの大きさは、
magnitude = sqrt(5 * 5 + (-3) * (-3)) magnitude = sqrt(25 + 9) magnitude = sqrt(34) magnitude = 5.8309518948453
となります。
正規化すると、
identity.x = 5 / 5.8309518948453 identity.y = -3 / 5.8309518948453 identity.x = 0.8574929257125442 identity.y = -0.5144957554275265
となり、これを「方向」とします。
現在位置に「方向(正規化した単位ベクトル)」を加算すると、移動後の座標が求められます。
移動後のX座標 = 移動前のX座標 + 方向のX成分 移動後のY座標 = 移動前のY座標 + 方向のY成分
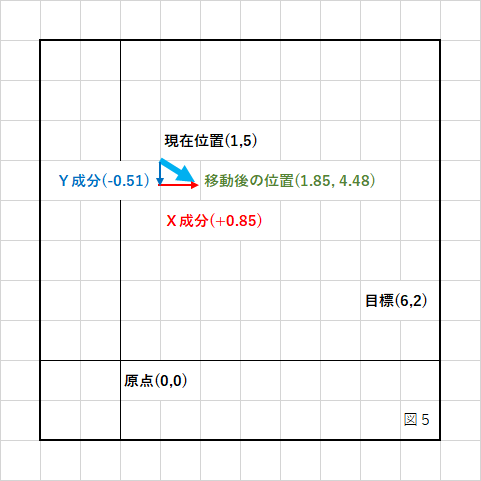
図4のケースで実際に移動後の座標を計算すると、
new_position.x = 1 + 0.8574929257125442 new_position.y = 5 + (-0.5144957554275265) new_position.x = 1.857492925712544 new_position.y = 4.485504244572473
となります。
C言語で書くと、
#include <math.h>
//現在位置
struct Vector2 position = { 1, 5 };
//目標地点
struct Vector2 destination = { 6, 2 };
//成分
struct Vector2 components;
//大きさ
float magnitude;
//方向(単位ベクトル)
struct Vector2 direction;
//成分計算
components.x = destination.x - position.x;
components.y = destination.y - position.y;
//大きさ計算
magnitude = (float)sqrt(components.x * components.x + components.y * components.y);
//方向計算(正規化)
direction.x = components.x / magnitude;
direction.y = components.y / magnitude;
//移動後の位置を計算
position.x += direction.x;
position.y += direction.y;
|
となります。
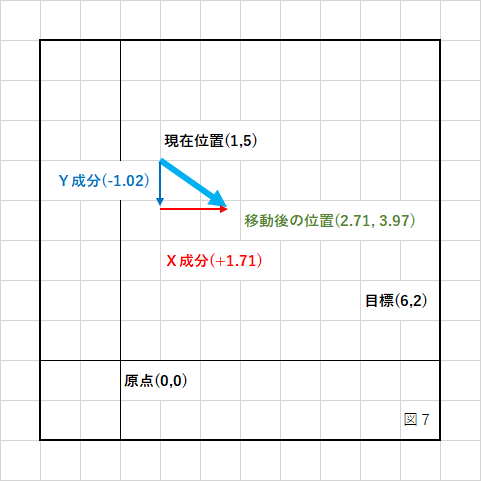
移動後の位置に繰り返し「方向ベクトル」を加算すると目標地点に近づいていきます。
また、「方向ベクトル」の大きさを変えることで、移動スピードを変えることができます。
例えば2倍のスピードで移動させたい場合は、
移動前のX座標 += 方向のX成分 * 2 移動前のY座標 += 方向のY成分 * 2
でOKです。
図4の例で実際の計算を行うと、
new_position.x = 1 + 0.8574929257125442 * 2 new_position.y = 5 + (-0.5144957554275265) * 2 new_position.x = 1 + 1.714985851425088 new_position.y = 5 + (-1.028991510855053) new_position.x = 2.714985851425088 new_position.y = 3.971008489144947
となります。
C言語で書くと、
float speed = 2; position.x += direction.x * speed; position.y += direction.y * speed; |
となります。
ベクトルを利用する場合、角度と合わせて利用するケースも多く見られます。
図2のケースで角度を求める計算を行ってみましょう。

今回計算したいケースは、図8の部分の角度(angle)です。
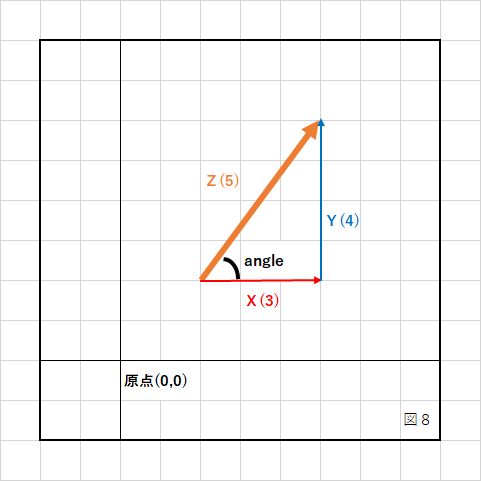
計算によって全ての辺の長さは分かっていますので、三角関数を使えば簡単に角度が求められます。
辺の長さから角度を求めるには、逆三角関数を使います。
1.Xの長さとYの長さが分かっている場合
atan アークタンジェント angle = arctan y / x
2.Xの長さとZの長さが分かっている場合
acos アークコサイン angle = arccos x / z
3.Yの長さとZの長さが分かっている場合
asin アークサイン angle = arcsin y / z
C言語で書くと、
#include <stdio.h>
#include <math.h>
float x = 3;
float y = 4;
float z = 5;
float angle;
angle = (float)atan(y / x);
printf("angle(atan) = %f\n", angle);
angle = (float)acos(x / z);
printf("angle(acos) = %f\n", angle);
angle = (float)asin(y / z);
printf("angle(asin) = %f\n", angle);
|
となります。
しかし、実際にプログラムを実行した結果を見ると、
<実行結果>
angle(atan) = 0.927295 angle(acos) = 0.927295 angle(asin) = 0.927295
と表示されます。
図の角度が0.9°というのは考えられませんが、これには理由があります。
ここで計算された結果は「ラジアン角」と言って、皆さんが小学校で習った0°〜360°の表記とは異なる表記になっています。
デグリー角は、皆さんが慣れている0°〜360°で表記する方法です。
対してラジアン角は0〜2π(パイ)で表記します。
角度の表記の違いを「単位円」という半径が1の円を使って説明します。

半径を表している青い線を反時計回りに45°回転すると図10のようになります。
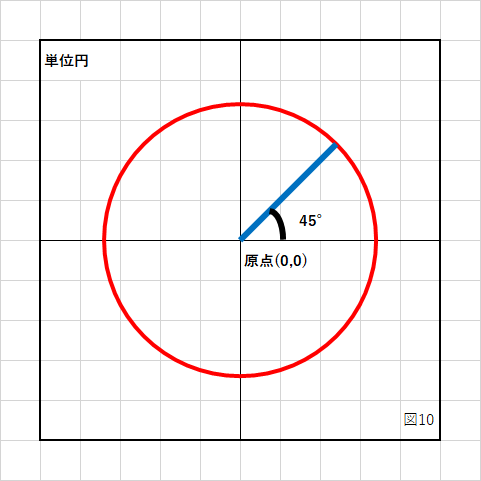
この時の円弧の長さ(図11の緑の部分)がラジアン角になります。
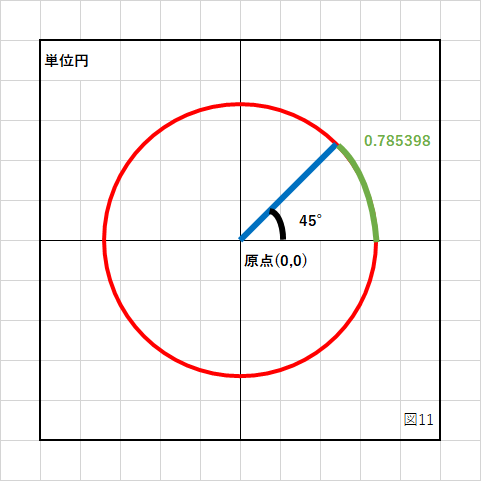
円周の長さは次の式で求められます。
円周の長さ = 半径 * 2 * π
学校では2πrと習ったと思います。
デグリー角とラジアン角を比較すると、
| デグリー角 | ラジアン角 |
| 0° | 0 |
| 90° | π/2 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
となります。
図11の円弧の長さは「0.785398」と書いてありますが、どのように計算したのでしょうか。
デグリー角360°をラジアン角2πにするためには、
360 / 180 * π = 2π
この式で変換できそうです。
言葉で書くと、
デグリー角 / 180 * π = ラジアン角
です。
書き方を変えると、
ラジアン角 = デグリー角 * π / 180
となります。
逆にラジアン角をデグリー角に変換するには、
デグリー角 = ラジアン角 * 180 / π
となります。
C言語で書くと、
#include <stdio.h>
float degree;
float radian;
//デグリー角45°を設定
degree = 45;
//デグリー角からラジアン角に変換
radian = degree * 3.14159265358979323846f / 180.0f;
printf("radian = %f\n", radian);
//ラジアン角からデグリー角に変換
degree = radian * 180.0f / 3.14159265358979323846f;
printf("degree = %f\n", degree);
|
<実行結果>
radian = 0.785398 degree = 45
となります。
プログラムで三角関数を使う場合、ラジアン角を使わなければなりませんので、この変換の式は重要です。
ベクトルを回転させるには三角関数のsinとcosを使います。
また「単位円」で説明します。

元と書いてある緑の線から反時計回りに45°回転させた後の緑の線を見てください。
回転後のX座標を示しているのが青い線で、これがcosの値です。
回転後のY座標を示しているのが赤い線で、これがsinの値です。
C言語で書いて実行すると↓のようになります。
#include <stdio.h>
#include <math.h>
Vector2 point;
float angle;
//デグリー角45°をラジアン角へ変換
angle = 45 * 3.14159265358979323846f / 180.0f;
//cos45°をX座標へ
point.x = (float)cos(angle);
//sin45°をY座標へ
point.y = (float)sin(angle);
printf("x = %f\n", point.x);
printf("y = %f\n", point.y);
|
<実行結果>
x = 0.707107 y = 0.707107
一応斜辺の長さを計算してみましょう。
//長さ(大きさ)を計算
float length = (float)sqrt(point.x * point.x + point.y * point.y);
printf("length = %f\n", length);
|
<実行結果>
length = 1.000000
このsinとcosの値を0°から360°まで表したのが下のグラフです。
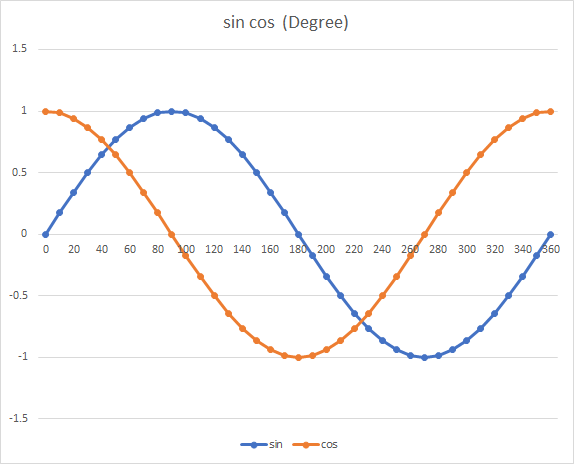
X座標を表すcosは1から−1になるまで減っていき、その後1へ向かって増えていきます。
Y座標を表すsinは0から1へ増えた後、−1まで減り、その後0へ戻っていきます。
これを利用して座標を回転させます。
しかし、sinやcosが表しているのは「単位円」での座標であり、このままでは任意の座標を回転させることはできません。
「単位円」は半径が決まっており、sinとcosで簡単に座標が求められますが、
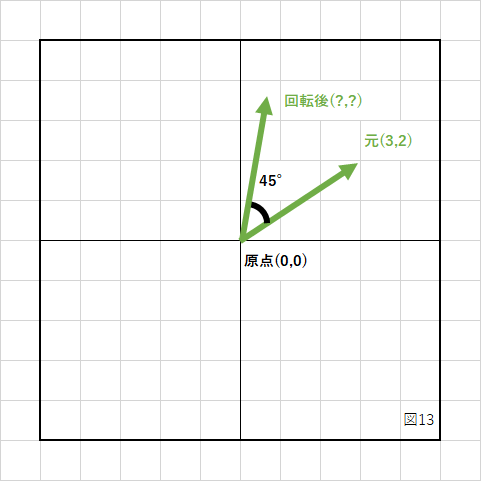
上の図のように元の座標(3,2)を反時計回りに45°回転させた後の座標が求めたいのです。
この計算には次の公式を使います。
回転後のX座標 = 回転前のX座標 * cos(回転角度) − 回転前のY座標 * sin(回転角度) 回転後のY座標 = 回転前のX座標 * sin(回転角度) + 回転前のY座標 * cos(回転角度)
数式で書くと、
x' = x * cosθ - y * sinθ y' = x * sinθ + y * cosθ
です。
C言語で書いて実行すると↓のようになります。
#include <stdio.h>
#include <math.h>
//元の座標
Vector2 befor = { 3, 2 };
//回転後の座標
Vector2 after;
//デグリー角45°をラジアン角へ変換
float angle = 45 * 3.14159265358979323846f / 180.0f;
//回転後の座標を計算
after.x = (float)(befor.x * cos(angle) - befor.y * sin(angle));
after.y = (float)(befor.x * sin(angle) + befor.y * cos(angle));
printf("x = %f\n", after.x);
printf("y = %f\n", after.y);
|
<実行結果>
x = 0.707107 y = 3.535534

これで回転できるようになりますが、タイトルにもあるようにあくまでも「原点中心」の回転になります。
原点中心の回転は上に書いた式で計算できますが、下図のような場合は通用しません。
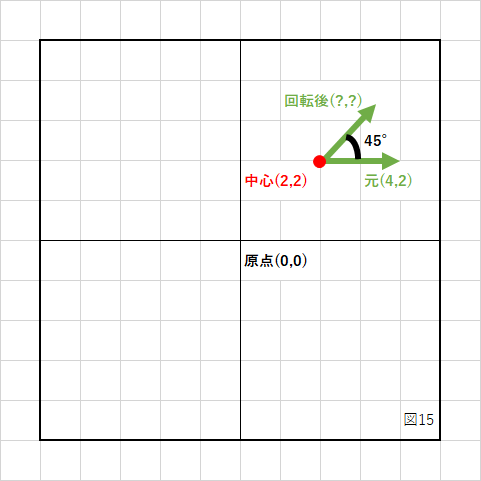
回転の中心座標が原点以外の場合は、次のように考えます。
1.回転の中心が原点になるよう、元の座標から中心座標を引く
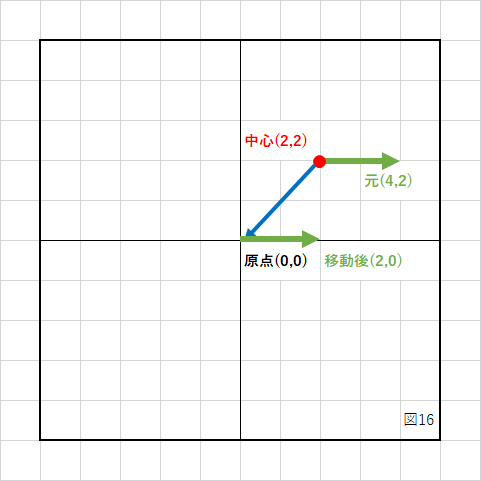
2.原点中心に回転させる
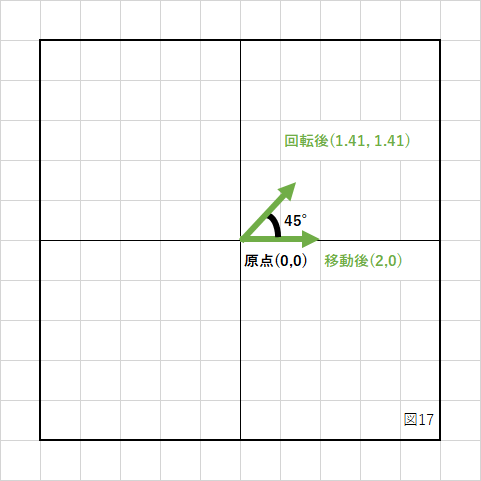
3.元の中心座標を加算して、位置を戻す
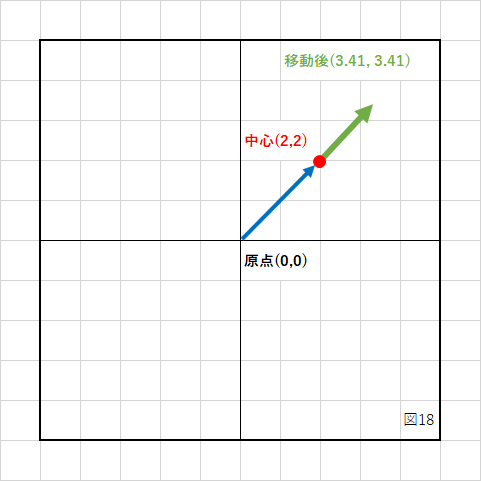
C言語で書いて実行すると↓のようになります。
#include <stdio.h>
#include <math.h>
//回転前の座標
Vector2 befor = { 4, 2 };
//回転の中心座標
Vector2 center = { 2, 2 };
//回転後の座標
Vector2 after;
//デグリー角45°をラジアン角へ変換
float angle = 45 * 3.14159265358979323846f / 180.0f;
//原点が回転の中心になるよう移動
befor.x -= center.x;
befor.y -= center.y;
//原点を中心に回転
after.x = (float)(befor.x * cos(angle) - befor.y * sin(angle));
after.y = (float)(befor.x * sin(angle) + befor.y * cos(angle));
//元の位置に移動
after.x += center.x;
after.y += center.y;
printf("x = %f\n", after.x);
printf("y = %f\n", after.y);
|
<実行結果>
x = 3.414214 y = 3.414214
内積はベクトル計算において重要な役割を持っています。
計算式は単純で、ベクトルAとベクトルBの内積は次の計算式です。
内積 = ベクトルAのX座標 * ベクトルBのX座標 + ベクトルAのY座標 * ベクトルBのY座標
これを、
内積 = ベクトルA ・ ベクトルB
と表し、演算子の「・」の形で「ドット(Dot)」と呼びます。
この計算式が何の役に立つかというと、
などがあります。
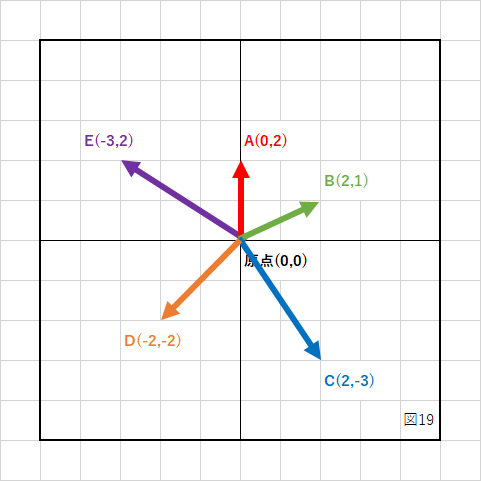
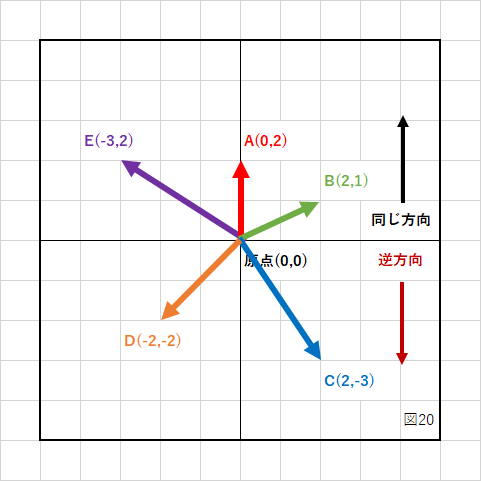
上の図の赤いベクトルAを基準として、他のベクトルとの内積の結果を表示してみます。
#include <stdio.h>
Vector2 a = { 0, 2 };
Vector2 b = { 2, 1 };
Vector2 c = { 2, -3 };
Vector2 d = { -2, -2 };
Vector2 e = { -3, 2 };
//a ・ b
float ab = a.x * b.x + a.y * b.y;
printf("a ・ b = %f\n", ab);
//a ・ c
float ac = a.x * c.x + a.y * c.y;
printf("a ・ c = %f\n", ac);
//a ・ d
float ad = a.x * d.x + a.y * d.y;
printf("a ・ d = %f\n", ad);
//a ・ e
float ae = a.x * e.x + a.y * e.y;
printf("a ・ e = %f\n", ae);
|
<実行結果>
a ・ b = 2.000000 a ・ c = -6.000000 a ・ d = -4.000000 a ・ e = 4.000000
これで何が分かるかというと、赤いベクトルと同じ方向を向いているベクトル(BとE)は結果が正(+)で、逆向きのベクトル(CとD)は結果が負(−)になってるということです。
これを利用して次のようなことができるようになります。
自分は原点にいて、Y軸の+方向を向いているとします。
また、座標上に敵が4体存在し、それぞれの座標を表します。
方向は単位ベクトルを使いますので、下の図のようなイメージです。
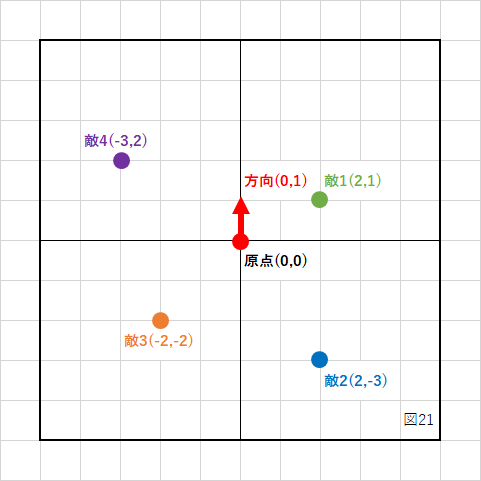
自分の前方向と敵へのベクトルとの内積を計算すれば、敵1と4は前方に、敵2と3は後ろにいることが分かります。
実際にC言語で書いて計算すると、
#include <stdio.h>
//前方向
Vector2 direction = { 0, 1 };
//敵の座標
Vector2 enemy1 = { 2, 1 };
Vector2 enemy2 = { 2, -3 };
Vector2 enemy3 = { -2, -2 };
Vector2 enemy4 = { -3, 2 };
float result;
result = direction.x * enemy1.x + direction.y * enemy1.y;
printf("direction ・ enemy1 = %f\n", result);
result = direction.x * enemy2.x + direction.y * enemy2.y;
printf("direction ・ enemy2 = %f\n", result);
result = direction.x * enemy3.x + direction.y * enemy3.y;
printf("direction ・ enemy3 = %f\n", result);
result = direction.x * enemy4.x + direction.y * enemy4.y;
printf("direction ・ enemy4 = %f\n", result);
|
<実行結果>
direction ・ enemy1 = 1.000000 direction ・ enemy2 = -3.000000 direction ・ enemy3 = -2.000000 direction ・ enemy4 = 2.000000
結果の正負で、前方か後方かが分かります。
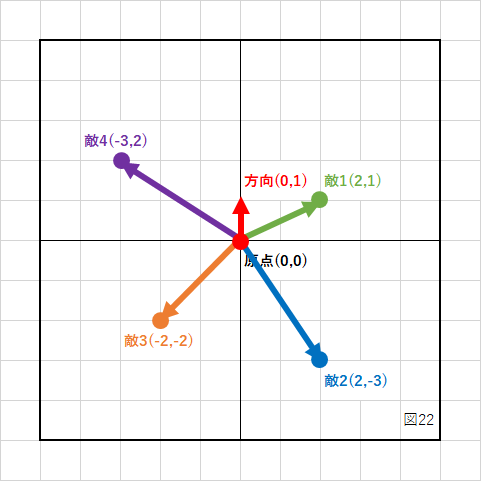
※真横にいた場合は結果が0になります。
しかし、自分が原点以外にいた場合はどうでしょうか?
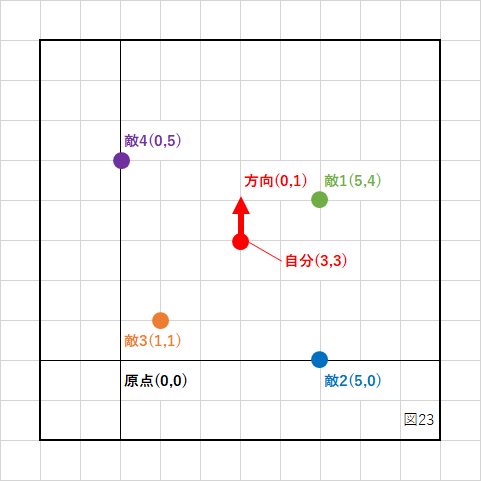
上の図のように自分の座標が(3,3)だった場合、このまま計算すると以下のようになります。
#include <stdio.h>
//前方向
Vector2 direction = { 0, 1 };
//敵の座標
Vector2 enemy1 = { 5, 4 };
Vector2 enemy2 = { 5, 0 };
Vector2 enemy3 = { 1, 1 };
Vector2 enemy4 = { 0, 5 };
float result;
result = direction.x * enemy1.x + direction.y * enemy1.y;
printf("direction ・ enemy1 = %f\n", result);
result = direction.x * enemy2.x + direction.y * enemy2.y;
printf("direction ・ enemy2 = %f\n", result);
result = direction.x * enemy3.x + direction.y * enemy3.y;
printf("direction ・ enemy3 = %f\n", result);
result = direction.x * enemy4.x + direction.y * enemy4.y;
printf("direction ・ enemy4 = %f\n", result);
|
<実行結果>
direction ・ enemy1 = 4.000000 direction ・ enemy2 = 0.000000 direction ・ enemy3 = 1.000000 direction ・ enemy4 = 5.000000
敵1,3,4は前(+)にいて、敵2は真横(0)にいるという結果になりました。
これは自分の位置を計算に入れていないため、原点から計算した結果になっています。
自分の方向も含めて、ベクトルの数値を座標に置き換えて表示すると下のようになります。
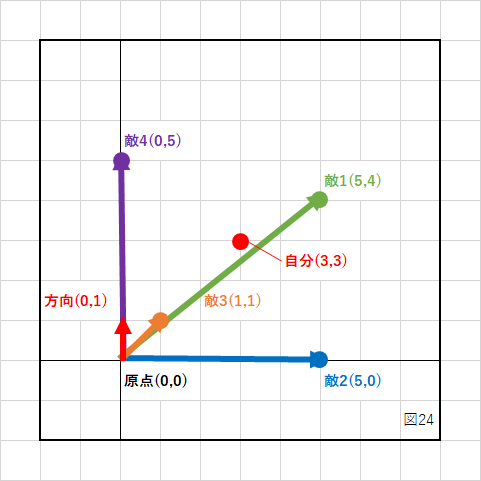
まず、方向ベクトルは単位ベクトルであり、基本的には原点を基準としています。
また、敵の座標も原点を中心とした座標であり、自分を中心にした座標ではありません。
自分との前後関係を計算したいのであれば、自分を中心にするように調整を行う必要があります。
自分から見た敵の方向を計算するには、自分が原点からどのくらい離れているかを計算に入れなければなりません。
自分は(3,3)にいますから、敵1は「自分からX方向に+2、Y方向に+1」離れていると考えます。
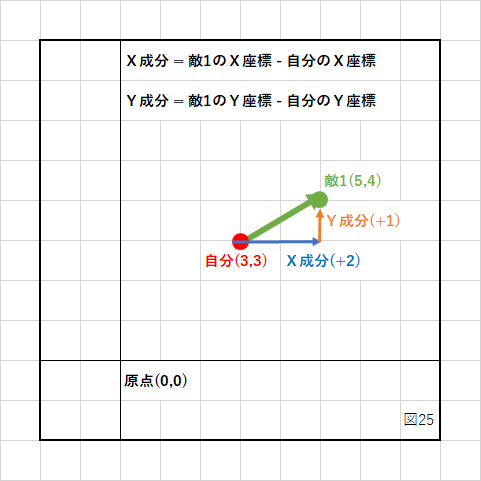
これは敵1の座標から自分の座標を引き算することで簡単に求まります。
すべての敵にこの計算を行うことで自分があたかも原点にいるような座標に変えることができます。
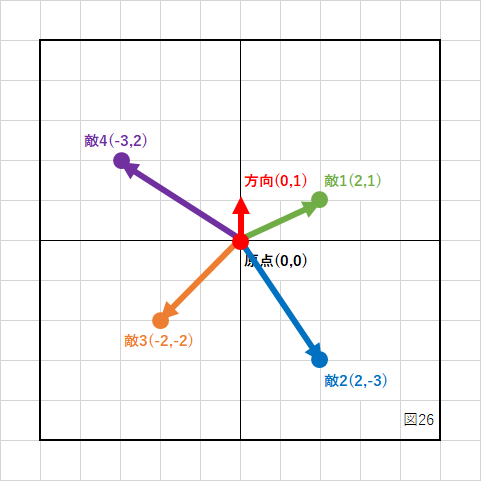
これをC言語で書いて実行すると、
#include <stdio.h>
//前方向
Vector2 direction = { 0, 1 };
//自分の位置
Vector2 position = { 3, 3 };
//敵の座標
Vector2 enemy1 = { 5, 4 };
Vector2 enemy2 = { 5, 0 };
Vector2 enemy3 = { 1, 1 };
Vector2 enemy4 = { 0, 5 };
float result;
//自分からの相対座標
Vector2 relative;
relative.x = enemy1.x - position.x;
relative.y = enemy1.y - position.y;
result = direction.x * relative.x + direction.y * relative.y;
printf("direction ・ enemy1 = %f\n", result);
relative.x = enemy2.x - position.x;
relative.y = enemy2.y - position.y;
result = direction.x * relative.x + direction.y * relative.y;
printf("direction ・ enemy2 = %f\n", result);
relative.x = enemy3.x - position.x;
relative.y = enemy3.y - position.y;
result = direction.x * relative.x + direction.y * relative.y;
printf("direction ・ enemy3 = %f\n", result);
relative.x = enemy4.x - position.x;
relative.y = enemy4.y - position.y;
result = direction.x * relative.x + direction.y * relative.y;
printf("direction ・ enemy4 = %f\n", result);
|
<実行結果>
direction ・ enemy1 = 1.000000 direction ・ enemy2 = -3.000000 direction ・ enemy3 = -2.000000 direction ・ enemy4 = 2.000000
きちんと、自分からそれぞれの敵の前後関係を計算することができました。
ベクトルの計算を行うときは(回転の時もそうですが)原点を中心とした計算かどうかをよく考えてください。
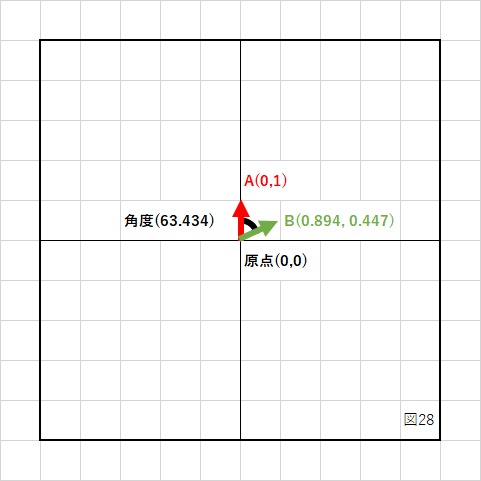
下の図のように2つのベクトルABがあり、その間の角度(黒い線)が知りたい場合があります。
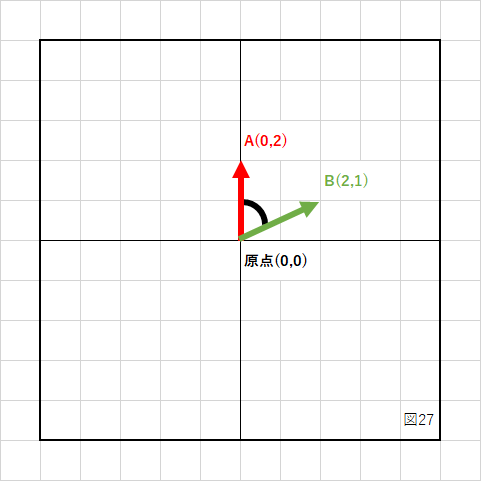
これを求めるために内積を使います。
より簡単に求めるために、2つのベクトルを単位ベクトルに変換します。
ベクトルA 変換前 (0, 2) 変換後 (0, 1)
ベクトルB 変換前 (2, 1) 変換後 (0.894,0.447)
この2つのベクトルの内積を計算します。
0 * 0.894 + 1 * 0.447 = 0.447
この数値を逆コサインを使って計算すると、角度(ラジアン角)が得られます。
acos(0.447) -> 1.107
これをデグリー角で表示すると、
63.434...
となります。
C言語で書いて実行してみます。
#include <stdio.h>
#include <math.h>
Vector2 a = { 0, 2 };
Vector2 b = { 2, 1 };
float magnitude;
//ベクトルAの正規化
magnitude = (float)sqrt(a.x * a.x + a.y * a.y);
a.x = a.x / magnitude;
a.y = a.y / magnitude;
//ベクトルBの正規化
magnitude = (float)sqrt(b.x * b.x + b.y * b.y);
b.x = b.x / magnitude;
b.y = b.y / magnitude;
//2つのベクトルの内積
float result = a.x * b.x + a.y * b.y;
//角度に変換
float angle = (float)acos(result);
//デグリー角に変換
printf("angle = %f\n", angle * 180.0f / 3.14159265358979323846f);
|
<実行結果>
angle = 63.434948
単位ベクトル同士で内積を計算すると下の図のようになります。
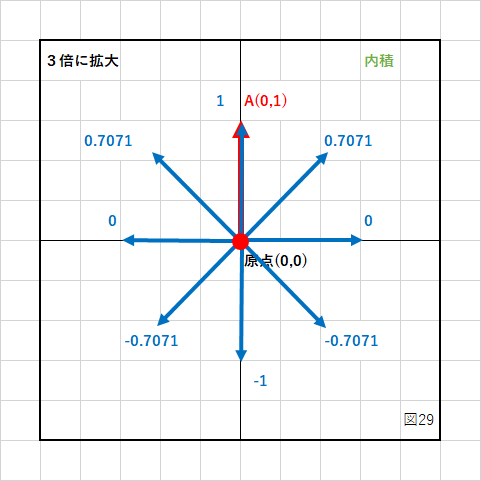
ベクトルA(赤いベクトル)はY軸の+方向を表しています。
青い矢印は45°間隔でベクトルを回転させたものです。
赤いベクトルと青いベクトルの内積結果が図に書いてある数値です。
前にも書きましたが、赤いベクトルと同じ方向を向いていれば+、逆方向は−、真横は0となります。
この数値の逆コサインを計算すると、
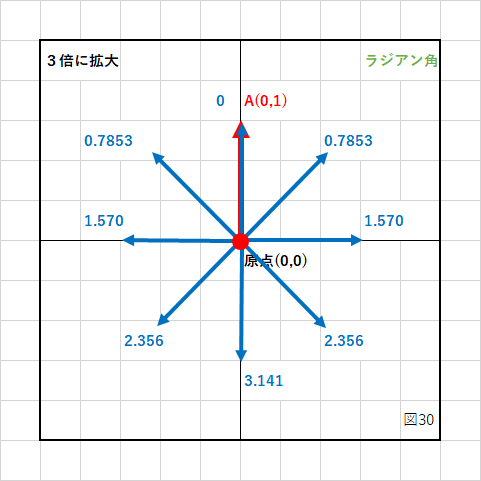
赤いベクトルから青いベクトルまでの角度がラジアン角で表示されます。
これをデグリー角に直すと、
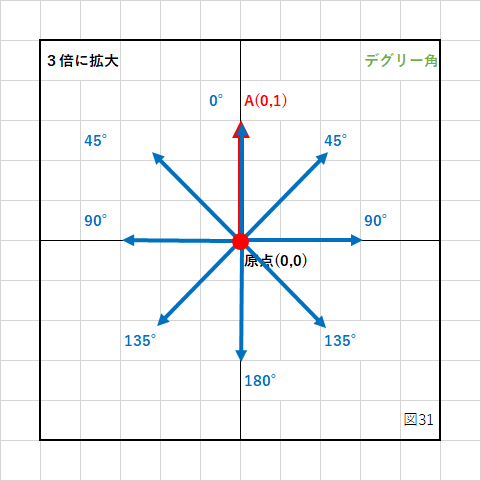
となります。
見てわかると思いますが、同じ45°という角度が左右にあるため、時計回りに45°か反時計回りに45°かの区別はつきません。
さて、これも「原点中心」の計算式のため、次のようなケースではそのまま使うことはできません。
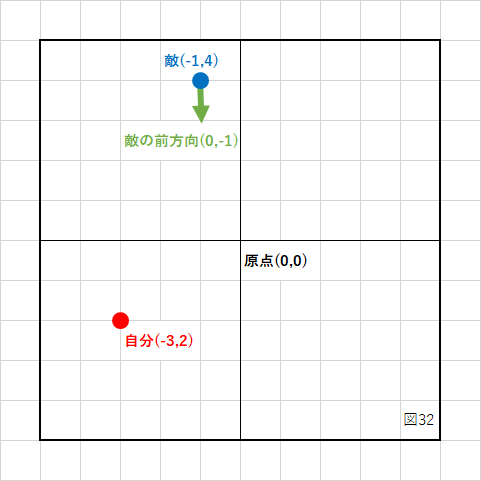
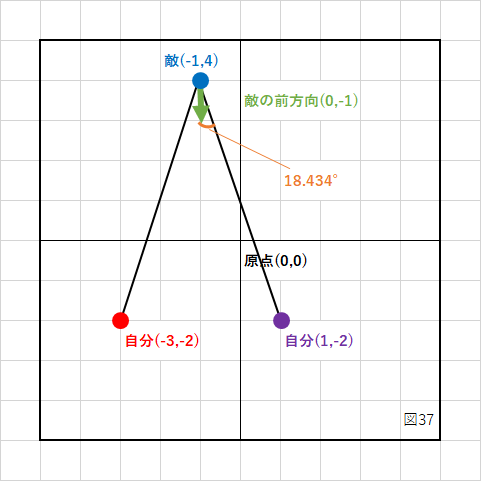
自分が(−3,2)の座標にいて、敵が(−1,4)にいます。
敵は真下(Y軸のマイナス方向)を向いている状態ですが、敵が自分の方に向くように回転させるには何度回転させれば良いでしょうか?

この場合は敵から自分へのベクトルを求めて、単位ベクトルに変換したものと、敵の前方向ベクトルの内積を計算することで求めることができます。
敵から自分へのベクトルを求めるには、単純に引き算すれば良いだけです。
前に書いた言葉で表すとベクトルの成分を求める式になります。
X成分 = 自分のX座標 − 敵のX座標 Y成分 = 自分のY座標 − 敵のY座標
実際の値を入れて計算すると、
(-3) - (-1) = -2 (-2) - 4 = -6
この座標を図にすると、
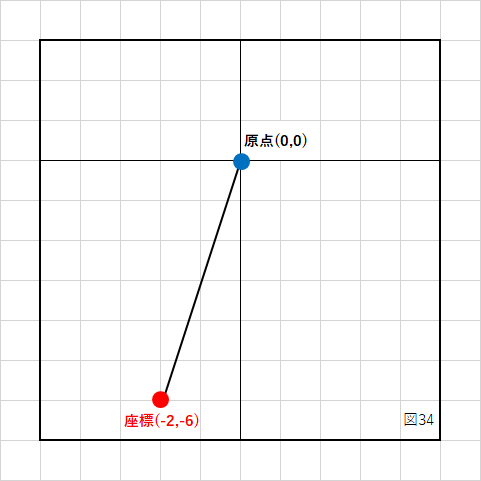
のように、敵を原点に置いた時の自分の座標に変換されます。
これを単位ベクトルに変換すると、
斜辺の長さ(ベクトルの大きさ)は「6.324555」ですから、
-2 / 6.324555 = -0.316228 -6 / 6.324555 = -0.948683
となります。
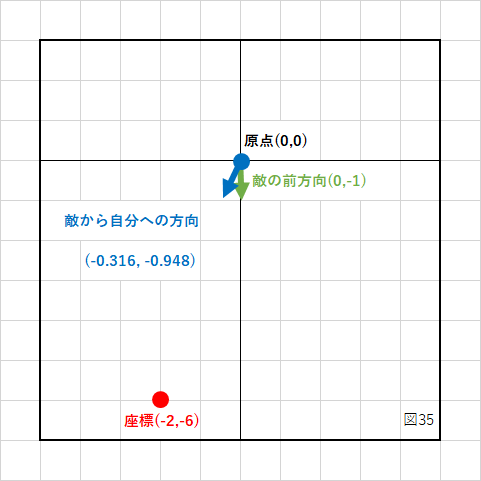
このベクトルと、敵の前方向のベクトルの内積を計算すると、
0 * -0.316228 + (-1) * (-0.948683) = 0.948683
となり、さらに逆コサインを計算することでラジアン角が求められます。
acos(0.948683) = 0.321751
さらにデグリー角に変換すると、
0.321751 * 180 / 3.14159265358979323846 = 18.434954
となり、「18.434954°」回転させることで敵が自分の方に向くことになります。
一連の計算をC言語で書いて実行すると、
#include <stdio.h>
#include <math.h>
//自分の位置
Vector2 myPos = { -3, -2 };
//敵の位置
Vector2 enemyPos = { -1, 4 };
//敵の前方向
Vector2 enemyDir = { 0, -1 };
//成分
Vector2 components;
//成分計算
components.x = myPos.x - enemyPos.x;
components.y = myPos.y - enemyPos.y;
//大きさ計算
float magnitude = (float)sqrt(components.x * components.x + components.y * components.y);
//敵から自分へのベクトルを計算
Vector2 toMyPos;
toMyPos.x = components.x / magnitude;
toMyPos.y = components.y / magnitude;
//内積
float result = enemyDir.x * toMyPos.x + enemyDir.y * toMyPos.y;
//ラジアン角に変換
float angle = (float)acos(result);
//デグリー角を表示
printf("degree = %f\n", angle * 180.0f / 3.14159265358979323846f);
|
<実行結果>
degree = 18.434954
となります。
※分かりやすいようにデグリー角に変換していますが、ゲーム内で使用する際にはラジアン角までの計算でOKです。
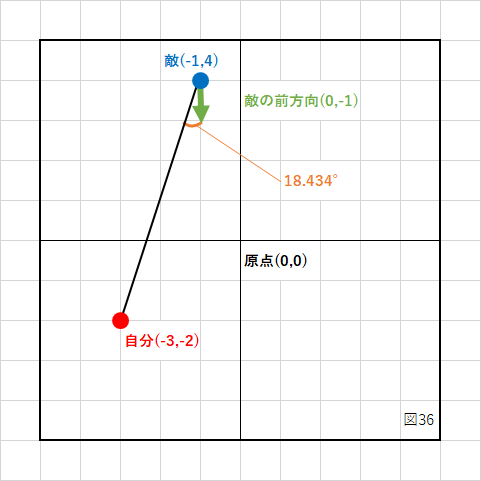
ただし、上にも書いたように時計回りに回転させるか、反時計回りに回転させるかは分かりません。
下の図のように、自分の座標(紫)が(1、−2)の場合も同じ角度が算出されます。
左右を判断する場合には後で説明する「外積」が必要となります。
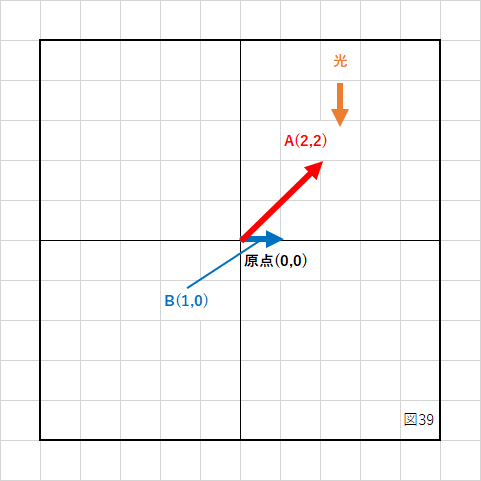
射影というより投影と言った方が分かりやすいかもしれません。
下の図のように、AB2つのベクトルがあるとします。
ベクトルBに対して垂直に光を当てた場合、ベクトルAの影がベクトルBに映るとイメージして、その影の長さを内積で求めることができます。

図のベクトルABの内積を計算してみると、
内積 = A.x * B.x + A.y * B.y
ですから、
2 * 4 + 2 * 0 = 8
全然違います。
影の長さを求めるためには、影が映るベクトル(B)を単位ベクトルにしなければなりません。
これで、
2 * 1 + 2 * 0 = 2
となり、きちんと影の長さが計算できました。
射影の使い道ですが、1つは垂線を求めるために使えます。
下の図は、点Aの位置が(1,2)であり、直線(3、−5)−(3,5)が青いベクトルで書かれています。
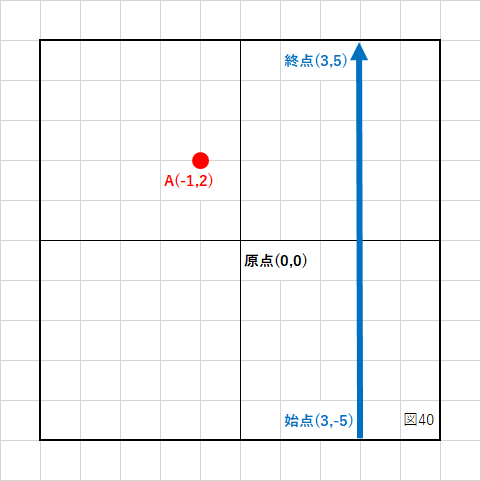
点Aから直線への最短距離(垂線の長さ)と交点(直線とAからの垂線が交わる座標)を求めたい場合、計算しなくても分かりますよね?
直線はY軸と並行ですから、始点と終点のX座標は変わりません。
図を見るだけで、最短距離は(4)であり、交点は(3,2)であることが分かります。
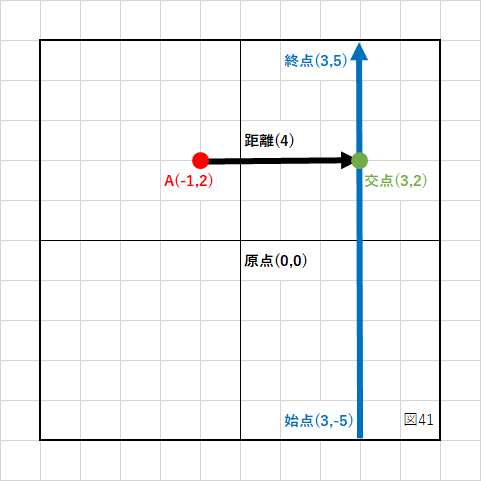
では、次の図の場合はどうでしょう?
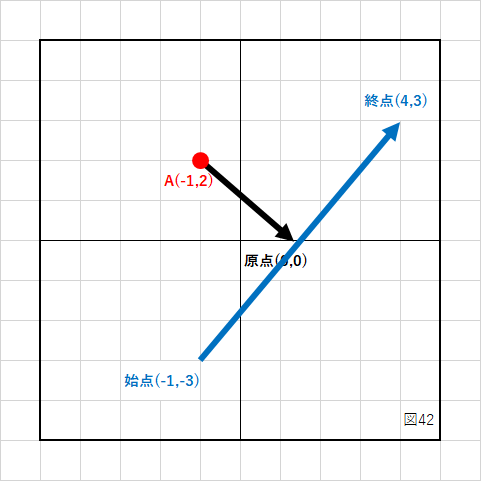
この場合、直線までの距離や交点を求めるのに、図を見ただけでは分かりません。
では、求め方を順番に説明していきましょう。
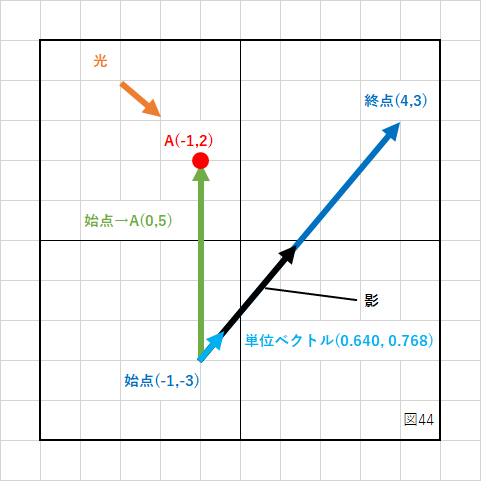
まず、直線の始点から点Aまでのベクトル(成分)を計算します。
X成分 = 点AのX座標 − 始点のX座標 Y成分 = 点AのY座標 − 始点のY座標
実際の値を入れてみると、
(-1) - (-1) = 0 2 - (-3) = 5
となり、緑のベクトルの成分は(0,5)になりました。

次に直線の始点と終点から成分を計算します。
X成分 = 終点のX座標 − 始点のX座標 Y成分 = 終点のY座標 − 始点のY座標
実際の値を入れてみると、
4 - (-1) = 5 3 - (-3) = 6
となり始点→終点の成分は(5,6)となります。
次に直線を正規化し、単位ベクトルにします。
直線の成分からベクトルの大きさを計算すると、
sqrt(5 * 5 + 6 * 6) = sqrt(25 + 36) = sqrt(61) = 7.810250
となり、単位ベクトルは、
5 / 7.810250 = 0.640184 6 / 7.810250 = 0.768221
となりました。
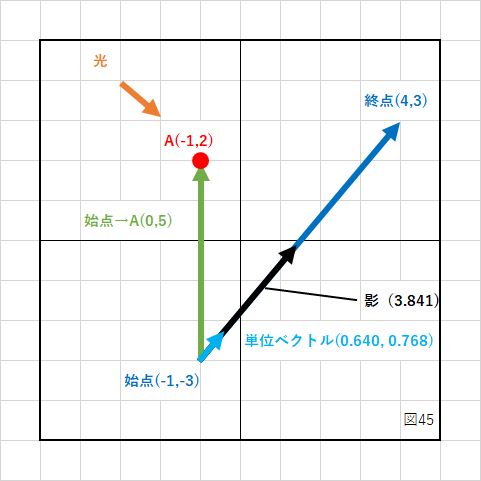
上の図を見ると、射影が使えるのが分かりますね。
始点→点Aのベクトルと直線の単位ベクトルの内積を計算すれば、影の長さが分かります。
内積を計算します。
影の長さ = 始点→点AのX成分 * 単位ベクトルのX成分 + 始点→点AのY成分 * 単位ベクトルのY成分
実際の数値を入れると、
0 * 0.640184 + 5 * 0.768221 = 3.841106
となりました。
しかし、影の長さだけですから、まだ点Aからの距離も交点も分かりません。
前に「単位ベクトルを使った移動」について説明しました。
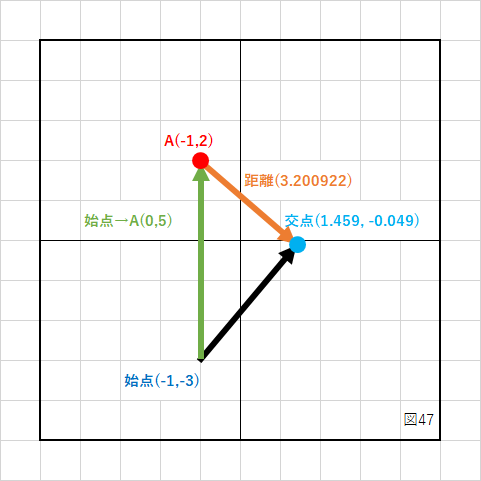
これを使えば交点が分かります。
図45の「始点」を「移動前の位置」、「単位ベクトル」を「方向」、「影の長さ」を「スピード」と置き換えればOKです。
移動後のX座標 = 移動前のX座標 + 方向のX成分 * スピード 移動後のY座標 = 移動前のY座標 + 方向のY成分 * スピード
これを数値で表すと、
(-1) + 0.640184 * 3.841106 = 1.459016 (-3) + 0.768221 * 3.841106 = -0.049181
となり、この移動後の座標が交点(1.459016,-0.049181)です。

交点が分かれば、交点と点Aの距離を求めれば良いだけですから、2つの座標から成分を計算し、ベクトル大きさを求めればOKです。
距離の求め方は、前に書いているのでここでは省略します。
最後に、C言語で書いて実行します。
#include <stdio.h>
#include <math.h>
Vector2 a = { -1, 2 };
Vector2 start = { -1, -3 };
Vector2 end = { 4, 3 };
//直線の始点から点Aへのベクトルの成分を計算
Vector2 startToA;
startToA.x = a.x - start.x;
startToA.y = a.y - start.y;
//直線の始点から終点へのベクトル(成分)を計算
Vector2 direction;
direction.x = end.x - start.x;
direction.y = end.y - start.y;
//正規化し単位ベクトルにする
float magnitude;
magnitude = (float)sqrt(direction.x * direction.x + direction.y * direction.y);
direction.x = direction.x / magnitude;
direction.y = direction.y / magnitude;
//影の長さを求める
float shadowLength = startToA.x * direction.x + startToA.y * direction.y;
//交点を求める
Vector2 crossPoint;
crossPoint.x = start.x + direction.x * shadowLength;
crossPoint.y = start.y + direction.y * shadowLength;
printf("cross point x = %f : y = %f\n", crossPoint.x, crossPoint.y);
//距離を求める
Vector2 crossPointToA;
crossPointToA.x = crossPoint.x - a.x;
crossPointToA.y = crossPoint.y - a.y;
float distance = (float)sqrt(crossPointToA.x * crossPointToA.x + crossPointToA.y * crossPointToA.y);
printf("distance = %f\n", distance);
|
<実行結果>
cross point x = 1.459016 : y = -0.049181 distance = 3.200922
この射影という考え方を利用することで、「円と線分の衝突判定」や「回転する四角形同士の衝突判定」などが可能になります。
外積もベクトル計算において重要な役割を持っています。
しかし、2次元と3次元の外積については大きく異なる部分があります。
さらに座標系という考え方にも左右されます。
ここでは左手座標系をベースにした2次元ベクトルの外積について説明します。
※DirectXが左手座標系のため
計算式は単純で、ベクトルAとベクトルBの外積は次の計算式です。
外積 = ベクトルAのX座標 * ベクトルBのY座標 − ベクトルAのY座標 * ベクトルBのX座標
これを、
外積 = ベクトルA × ベクトルB
と表し、演算子の「×」の形で「クロス(Cross)」と呼びます。
この計算式が何の役に立つかというと、
などがあります。
まず、左手座標系とは何かを説明します。
左手座標系は3次元の座標を表す言葉の1つで、下の図のような考え方です。
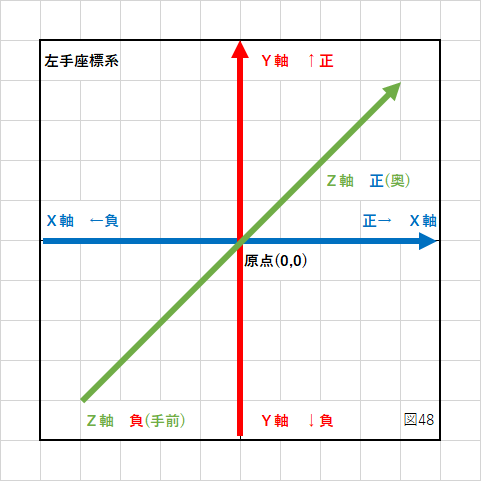
Z軸の正(プラス方向)が画面の奥側になります。
これに対して右手座標系はZ軸の向きが逆です。
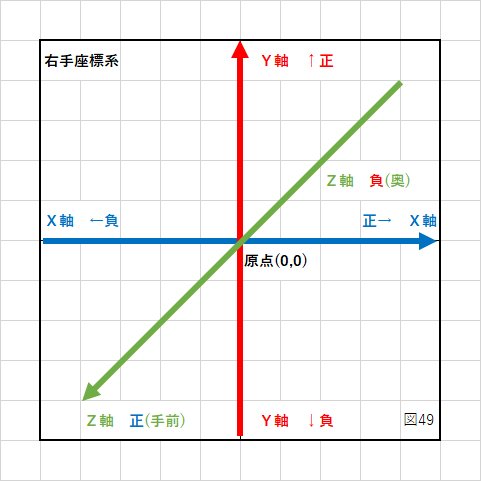
この定義があいまいだと外積の結果が一定では無くなります。
今回は「左手座標系」での説明になります。
内積でも同じことを行いましたが、垂線の高さを求めるだけであれば外積の方が楽です。
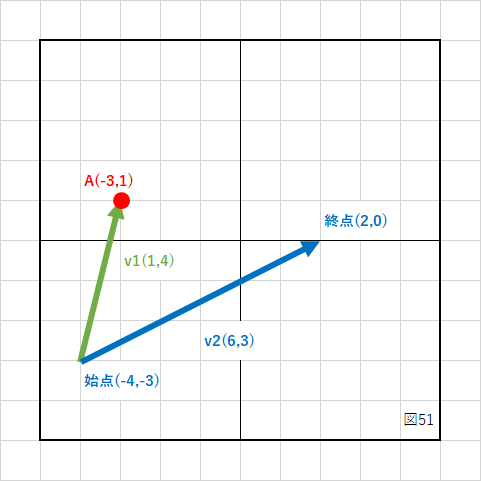
下の図の黒い矢印の長さを求めたいとします。

まず、内積の時と同じように、直線の始点から点Aまでのベクトル(成分)を計算します。
X成分 = 点AのX座標 − 始点のX座標 Y成分 = 点AのY座標 − 始点のY座標
実際の値を入れてみると、
(-3) - (-4) = 1 1 - (-3) = 4
となり、緑のベクトル(v1とします)の成分は(1,4)になりました。
次に直線の始点と終点から成分を計算します。
X成分 = 終点のX座標 − 始点のX座標 Y成分 = 終点のY座標 − 始点のY座標
実際の値を入れてみると、
2 - (-4) = 6 0 - (-3) = 3
となり始点→終点(v2とします)の成分は(6,3)となりました。
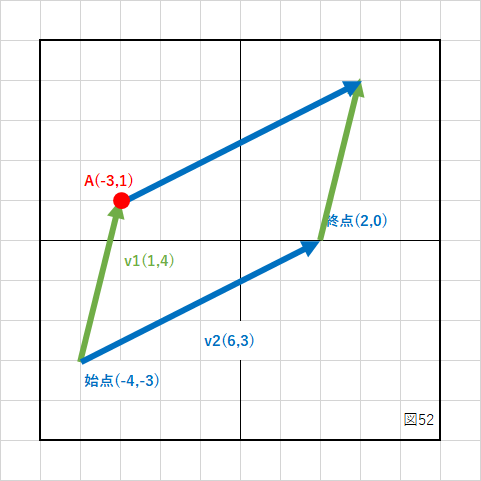
この2つベクトル(v1,v2)の外積を計算します。
上にも式を書きましたが、v1、v2を使って書き直すと、
外積 = v1 × v2 外積 = v1.x * v2.y - v1.y * v2.x
となり、数値を入れると、
1 * 3 - 4 * 6 = 3 - 24 = -21
となります。
ちなみに、v1とv2を入れ替えると、
外積 = v2 × v1 外積 = v2.x * v1.y - v2.y * v1.x 6 * 4 - 3 * 1 = 24 - 3 = 21
と「符号が変わり」ます。
これは非常に重要なのですが、垂線の高さには関係ないので置いておきましょう。
さて、外積の結果の「-21」や「21」ですが、これが何を表しているかと言うと、下の図のような「平行四辺形の面積」を表しています。
※面積が負の場合は絶対値を計算します。
平行四辺形の面積は「底辺×高さ」で求められます。
底辺は始点と終点のベクトル成分(v2)から、ベクトルの大きさを求めれば分かります。
底辺の長さ = 6.708204
面積は分かっていますから、
高さ = 面積 / 底辺
であり、
21 / 6.708204 = 3.130495
となりました。
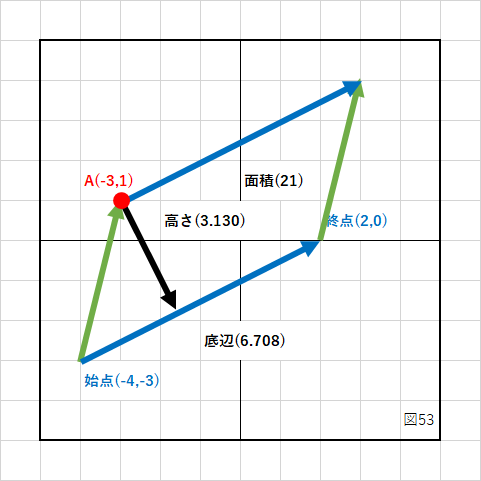
C言語で書いて実行してみます。
#include <stdio.h>
#include <math.h>
Vector2 a = { -3, 1 };
Vector2 start = { -4, -3 };
Vector2 end = { 2, 0 };
//始点→点Aの成分計算
Vector2 startToA;
startToA.x = a.x - start.x;
startToA.y = a.y - start.y;
//始点→終点の成分計算
Vector2 startToEnd;
startToEnd.x = end.x - start.x;
startToEnd.y = end.y - start.y;
//外積(面積)を求める
float sum = startToEnd.x * startToA.y - startToEnd.y * startToA.x;
//底辺(startToEnd)の大きさ計算
float magnitude;
magnitude = (float)sqrt(startToEnd.x * startToEnd.x + startToEnd.y * startToEnd.y);
printf("%f\n", sum / magnitude);
|
<実行結果>
3.130495
内積のところで行った計算でも同じ結果が得られますので、試してみてください。
左右判定を行う前に座標系について重要な説明をしておきます。
垂線の高さの計算のところで面積を求める際に、外積計算の順番を入れ替えると結果の符号が変わることを説明しました。
左手座標系の場合、下の図のようになることを覚えておいてください。
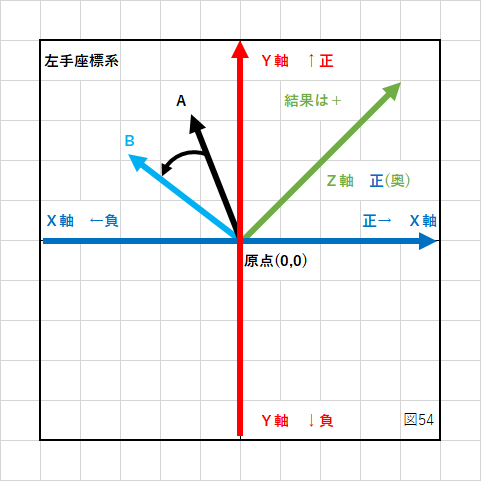
ベクトルA×ベクトルBの順番で「反時計回り」に計算した場合、結果は正(+)になります。
逆にベクトルB×ベクトルAの順番で「時計回り」に計算した場合、結果は負(−)になります。
内積と同じように単位ベクトル同士の外積の結果を図にしてみましょう。
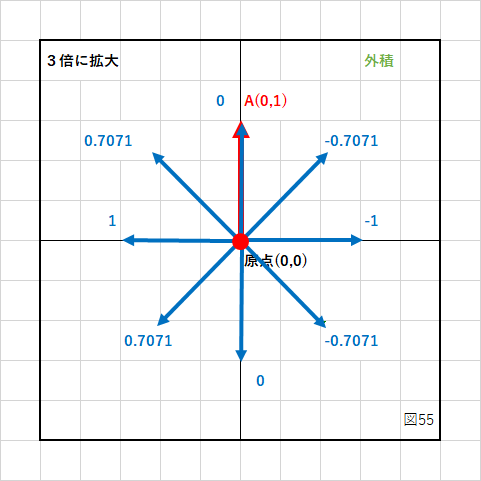
この図をみると、ベクトルAから見て「右側が正(+)」「左側が負(−)」になっていることが分かります。
真正面と真後ろは0になっていますね。
内積と組み合わせれば、自分と敵の位置関係がバッチリ分かります。
〇角形とは、三角形や四角形、五角形のことです。
ある点が、この図形の中にあるか、外にあるかを調べる時も外積が役に立ちます。
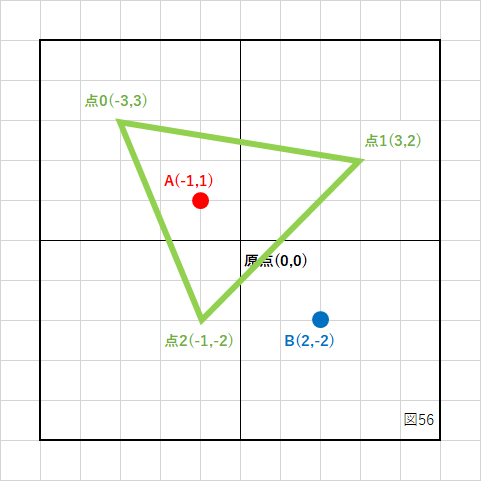
上の図の、点Aは三角形012に内包されていますが、点Bは内包されていません。
これを外積で判断します。
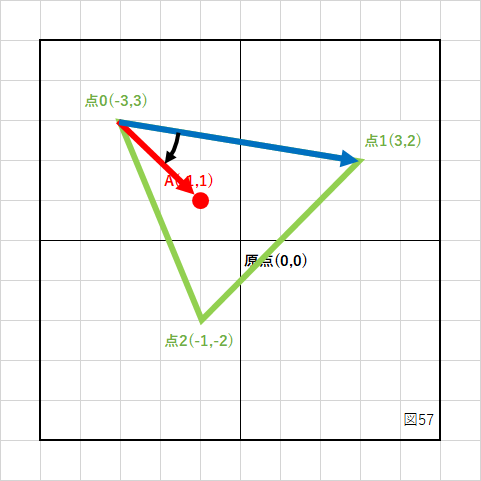
まず、点0と点1のベクトル成分(図の青いベクトル)を計算します。
同じく点0と点Aのベクトル成分(図の赤いベクトル)を計算します。
この2つのベクトルを「青×赤」の順番で外積計算します。
時計回りに計算することになるので、結果は負(−)になります。
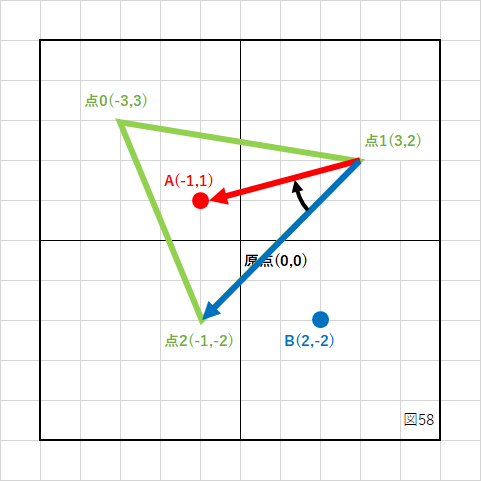
次に点1から点2のベクトル成分(図の青いベクトル)を計算します。
同じく点1から点Aのベクトル成分(図の赤いベクトル)を計算します。
この2つのベクトルを「青×赤」の順番で外積計算します。
時計回りに計算することになるので、これも結果は負(−)になります。

次に点2から点0のベクトル成分(図の青いベクトル)を計算します。
同じく点2から点Aのベクトル成分(図の赤いベクトル)を計算します。
この2つのベクトルを「青×赤」の順番で外積計算します。
時計回りに計算することになるので、これも結果は負(−)になります。
これら3つの結果が「全て負」になったので、点Aは三角形012に内包されています。
次に点Bについて同じように計算してみます。
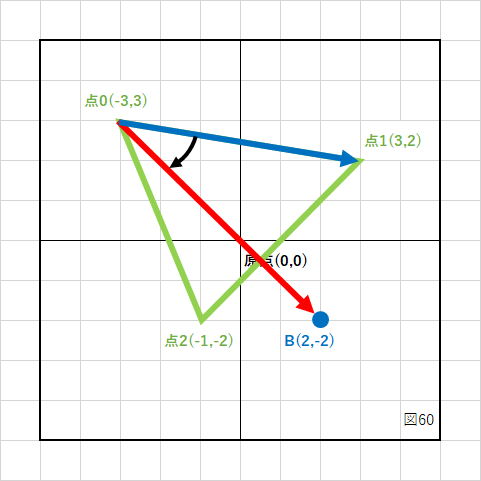
まず、点0と点1のベクトル成分(図の青いベクトル)を計算します。
同じく点0と点Bのベクトル成分(図の赤いベクトル)を計算します。
この2つのベクトルを「青×赤」の順番で外積計算します。
時計回りに計算することになるので、結果は負(−)になります。
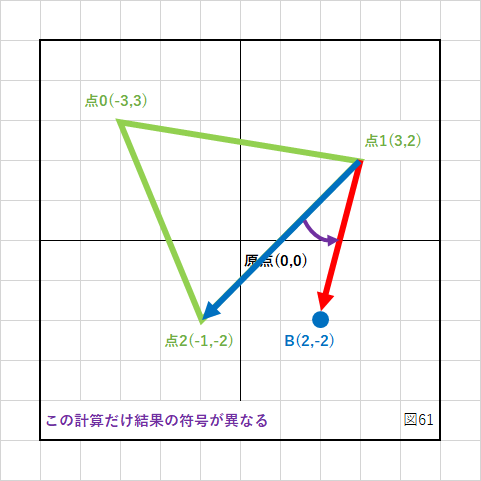
次に点1から点2のベクトル成分(図の青いベクトル)を計算します。
同じく点1から点Bのベクトル成分(図の赤いベクトル)を計算します。
この2つのベクトルを「青×赤」の順番で外積計算します。
「反時計回り」に計算することになるので、結果は正(+)になります。
次に点2から点0のベクトル成分(図の青いベクトル)を計算します。
同じく点2から点Bのベクトル成分(図の赤いベクトル)を計算します。
この2つのベクトルを「青×赤」の順番で外積計算します。
時計回りに計算することになるので、結果は負(−)になります。
3つの計算を行った結果、1つだけ結果が正(+)であったので、点Bは三角形012に内包されていません。
※三角形の頂点座標を時計回りに設定している場合の符号となります。
※頂点座標を反時計回りにした場合は、符号が逆になりますので気を付けましょう。
この方法を使えば、四角形でも五角形でも同じように求められます。
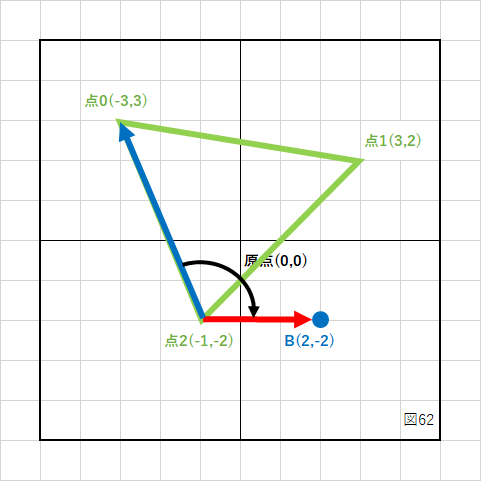
点AのケースをC言語で書いて実行してみます。
#include <stdio.h>
//調べる点の座標
Vector2 pointA = { -1, 1 };
//三角形の頂点座標配列(時計回りに設定)
Vector2 triangle[3] = {
{ -3, 3 },
{ 3, 2},
{ -1, -2},
};
//3回分の結果を入れる配列
float result[3];
//作業用ベクトル
Vector2 v1;
Vector2 v2;
//点0→点1
v1.x = triangle[1].x - triangle[0].x;
v1.y = triangle[1].y - triangle[0].y;
//点0→点A
v2.x = pointA.x - triangle[0].x;
v2.y = pointA.y - triangle[0].y;
//外積計算
result[0] = v1.x * v2.y - v1.y * v2.x;
//点1→点2
v1.x = triangle[2].x - triangle[1].x;
v1.y = triangle[2].y - triangle[1].y;
//点1→点A
v2.x = pointA.x - triangle[1].x;
v2.y = pointA.y - triangle[1].y;
//外積計算
result[1] = v1.x * v2.y - v1.y * v2.x;
//点2→点0
v1.x = triangle[0].x - triangle[2].x;
v1.y = triangle[0].y - triangle[2].y;
//点2→点A
v2.x = pointA.x - triangle[2].x;
v2.y = pointA.y - triangle[2].y;
//外積計算
result[2] = v1.x * v2.y - v1.y * v2.x;
//3つの外積の結果、全ての符号が同じ場合「内包」
if ((result[0] < 0 && result[1] < 0 && result[2] < 0) ||
(result[0] > 0 && result[1] > 0 && result[2] > 0)) {
printf("Inside\n");
}
else {
printf("Outside\n");
}
|
<実行結果>
Inside
#include <stdio.h>
#include <math.h>
//PI
#define PI 3.14159265358979323846f
//ラジアン角→デグリー角
#define ToDegree(radian) (radian * 180.0f / PI)
//デグリー角→ラジアン角
#define ToRadian(degree) (degree * PI / 180.0f)
//構造体
struct Vector2 {
float x;
float y;
};
//加算
Vector2 Add(const Vector2 v1, const Vector2 v2)
{
Vector2 temp;
temp.x = v1.x + v2.x;
temp.y = v1.y + v2.y;
return temp;
}
//減算
Vector2 Sub(const Vector2 v1, const Vector2 v2)
{
Vector2 temp;
temp.x = v1.x - v2.x;
temp.y = v1.y - v2.y;
return temp;
}
//乗算
Vector2 Mul(const Vector2 v1, const float s)
{
Vector2 temp;
temp.x = v1.x * s;
temp.y = v1.y * s;
return temp;
}
//除算
Vector2 Div(const Vector2 v1, const float s)
{
Vector2 temp;
temp.x = v1.x / s;
temp.y = v1.y / s;
return temp;
}
//大きさを求める
float Magnitude(const Vector2 v)
{
return (float)sqrt(v.x * v.x + v.y * v.y);
}
//正規化
Vector2 Normalize(const Vector2 v)
{
Vector2 temp;
float length = Magnitude(v);
temp.x = v.x / length;
temp.y = v.y / length;
return temp;
}
//回転
Vector2 Rotate(const Vector2 v, const float angle)
{
Vector2 temp;
temp.x = (float)(v.x * cos(angle) - v.y * sin(angle));
temp.y = (float)(v.x * sin(angle) + v.y * cos(angle));
return temp;
}
//内積
float Dot(const Vector2 v1, const Vector2 v2)
{
return v1.x * v2.x + v1.y * v2.y;
}
//外積
float Cross(const Vector2 v1, const Vector2 v2)
{
return v1.x * v2.y - v1.y * v2.x;
}
//2点間の距離を求める
float Distance(const Vector2 v1, const Vector2 v2)
{
Vector2 temp;
temp.x = v2.x - v1.x;
temp.y = v2.y - v1.y;
return Magnitude(temp);
}
int main()
{
Vector2 v1 = { 2, 4 };
Vector2 v2 = { 6, 3 };
Vector2 v3;
//加算
v3 = Add(v1, v2);
//減算
v3 = Sub(v1, v2);
//乗算
v3 = Mul(v1, 5);
//除算
v3 = Div(v2, 3);
float result;
//大きさ(成分)
result = Magnitude(v1);
//正規化
v3 = Normalize(v1);
//回転
v3 = Rotate(v1, ToRadian(45));
//内積
result = Dot(v1, v2);
//外積
result = Cross(v1, v2);
//2点間の距離
result = Distance(v1, v2);
return 0;
}
|
#include <iostream>
#include <cmath>
//PI
const float PI = 3.14159265358979323846f;
//ラジアン角→デグリー角
float ToDegree(float radian)
{
return radian * 180.0f / PI;
}
//デグリー角→ラジアン角
float ToRadian(float degree)
{
return degree * PI / 180.0f;
}
//クラス
class Vector2
{
public:
float x;
float y;
Vector2() : x(0), y(0) {};
Vector2(const float x, const float y) : x(x), y(y) {};
//加算
Vector2 operator+(const Vector2 &rhs) const
{
return Vector2(x + rhs.x, y + rhs.y);
}
//減算
Vector2 operator-(const Vector2 &rhs) const
{
return Vector2(x - rhs.x, y - rhs.y);
}
//乗算
Vector2 operator*(const float rhs) const
{
return Vector2(x * rhs, y * rhs);
}
//除算
Vector2 operator/(const float rhs) const
{
return Vector2(x / rhs, y / rhs);
}
//大きさを求める
float Magnitude() const
{
return (float)sqrt(x * x + y * y);
}
//正規化
Vector2 Normalize() const
{
return *this / Magnitude();
}
//回転
Vector2 Rotate(float angle) const
{
return Vector2(
(float)(x * cos(angle) - y * sin(angle)),
(float)(x * sin(angle) + y * cos(angle)));
}
//内積
float Dot(const Vector2 &rhs) const
{
return x * rhs.x + y * rhs.y;
}
//外積
float Cross(const Vector2 &rhs) const
{
return x * rhs.y - y * rhs.x;
}
//2点間の距離を求める
float Distance(const Vector2 target) const
{
Vector2 temp = target - *this;
return temp.Magnitude();
}
};
int main()
{
Vector2 v1( 2, 4 );
Vector2 v2( 6, 3 );
Vector2 v3;
//加算
v3 = v1 + v2;
//減算
v3 = v1 - v2;
//乗算
v3 = v1 * 5;
//除算
v3 = v2 / 3;
float result;
//大きさ(成分)
result = v1.Magnitude();
//正規か
v3 = v1.Normalize();
//回転
v3 = v1.Rotate(ToRadian(45));
//内積
result = v1.Dot(v2);
//外積
result = v1.Cross(v2);
//2点間の距離
result = v1.Distance(v2);
return 0;
}
|